√100以上 正八角形 一辺の���さ 作図 218327-正八角形 一辺の長さ 作図

よって、求める8角形の ＝aとして、Rを使わずに面積を求める方法を考えます。 上の解説をそのまま生かして、一辺の長さをaとして aで面積を求めてみます。 見通し 基本的には、上の解説の通りですが、Rをaで表す事ができればよいわけです。 R＝h＋χ という性質を利用すれば解決でき正八十四角形 正八十四角形においては、中心角と外角は4285°で、内角は°となる。 一辺の長さが a の正八十四角形の面積 S は正十二面体の表面積、体積そして半径（内接円と外接円)を計算する前に、球を利 用して正十二面体を形成することを考えましょう。 正多面体の一つの頂点に対して 三つの正三角形や四つの正三角形が集まる形だと、それぞれ、正四面体や正八 面体にしかならないので、五つの正三角形が

小学5年生 正多角形 算数 Active Learning 学院

正八角形 一辺の長さ 作図

正八角形 一辺の長さ 作図-線分 ab を一辺とする正五角形を作図します。 をクリックして下さい。 (1) 線分 ab の垂直二等分線 l をひく。 (2) ab の中点 c を中心とする半径 ab の円弧を かき，l との交点を d とする。 (3) a，d を通る直線 m をひく。 (4) d を中心とする半径 ac の円弧をかき，m との 交点を e とする。 (5) a を中心 折り紙の一辺を「2」とします まずは完成形を見てください。 正五角形の対角線と折り紙の辺の長さが同じです。 したがって、正五角形の対角線の長さも「2」です。 ということは、一辺の長さが √ 51 の正五角形を作るということです。

正多角形 Ironcad ユーザーガイド

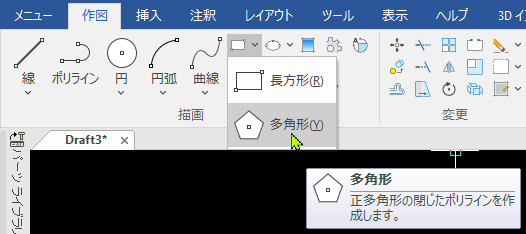
 一辺の長さがaである正n角形において、m個隣の頂点同士を結ぶ線分の長さを考えます。 図2 m個隣の頂点同士を結ぶ線分の長さ 図2はn=8、すなわち 正 八 角 形 の場合です。 正n角形の中心Oから、互いに隣り合う二つの頂点のそれぞれ(図2では例えば点A及び点B)に線分を引いてできる二11 – ポリゴン1 – 一辺の長さを指定して多角形を描く 11 – ポリゴン1 – 一辺の長さを指定して多角形を描く 辺の長さを指定して正三角形を描いてみましょう。 1 – 正三角形を作成します あらかじめ点が作図された図面ファイルを開きます。 画面左下にあるアプリケーションステータスここでは、半径1の円に内接する正五角形の一辺の長さを計算して、正五角形の作図方法を説明します。 正五角形の内角は 2π/5 2 π / 5 ラジアン（72°）であることから、 まず最初に a=cos(2π/5) a = cos ⁡ ( 2 π / 5) を使って一辺の長さを計算します。 右の図に

正八角形の外角が45°であることを考えると 四隅にある三角形は45°、45°、90°になっている特別な直角三角形であることが分かりますね。 だから、辺の比は \(11\sqrt{2}\) となるので このように辺の長さを求めることができます。直角三角形の辺の長さが2つ分かれば、もう1つも計算することができます。求め方と計算するためのツールを紹介します。 算数から高度な数学まで、網羅的に解説したサイト 直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学 > 図形 > 直角三角形の辺の長さの求め方と計算ツール八角形の面積(対辺) A A： 面積： 八角形の面積 (頂点) B B： 面積： 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 LC形 L形 C形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1

角の数が素数 p のものを正p角形と呼ぶ。 正p角形のうち、作図可能なものは、角（辺）の数 p がフェルマー素数 (3、5、17、257、) である場合のみであり、それぞれ正三角形、正五角形、正十七角形、正二百五十七角形、正六万五千五百三十七角形である。 角の数が素数でないものについては正八角形 正八角形においては、一つの外角と中心角は45 °で、内角は135°になる。 一辺の長さを a とすれば、周長は 8a 、面積 A は下記となる。 = = () (/) を有理数と平方根で表すことが可能である。= = = = 正八角形の作図Φ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r＝300でのn=8の多角形の1辺の長さaはではなくて？ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形と考えられます。

円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ

1

ただ、この作図に必要なのは、 垂線の作図;正八角形 正八角形 においては、一つの 外角 と 中心角 は 45 ° で、 内角 は135°になる。 一辺の長さを a とすれば、周長は 8a 、面積 A は下記となる。 A = 2 a 2 cot ⁡ π 8 = 2 ( 1 2 ) a 2 ≈ 4843 a 2 {\displaystyle A=2a^ {2}\cot {\frac {\pi } 正六角形の中に、同じ辺の長さの正三角形が6つ有るので、正三角形の面積が分かれば、その6倍が正六角形の面積となります。 以下が、正三角形の面積を計算する公式です。 正三角形の面積を6倍します。 この式をまとめると以下のようになります。この長さは、正五角形の一辺の長さに相当します。 次に間隔が長い鉛筆孔2つを選んで書きます。 この長さは、正五角形の対角線の長さに相当します。 交点を線で結んで完成です。 コンパスを使わずに星形正五角形を書くことができました。 娘がとても喜んだので、勝本さんはもっと多くの

コンパスと定規を使った七角形 正多角形 の描き方 図形の描き方016a 夏貸文庫

発展 円に内接する正五角形の作図 デザインあ おとなスペシャルで紹介されてたやつ なかけんの数学ノート

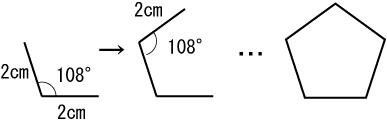
では、一辺3センチの正五角形の場合どんな大きさの円をかけばよいのでしょうか。 これが分かれば簡単ですね。 ☆ 求める計算式 比較的簡単な図形の問題です。 ここでは解説は省略しますが、次の式で求めることが出来ます。 R ＝ m／2sin（180／n） n：多角辺の長さ 等しい （例） 72° 108° 54° 60° 正三角形 1° 点 正多角形と円 1② ₁ にあてはまる言葉を書きましょう。 （ 点） の長さがすべて等しく，角の大きさも すべて 多角形を，正多角形といいます。 2 下の円を使って，正八角形をかきましょう。 （ 点） 3 下の図は正五角形です 13年06月19日 (水) 三角関数使って表記すれば半径1の円に内接する正N角形の一辺の長さは 2sin(π / N) なんですが、この値は具体的に加減乗除と累乗根を使って表すことができます。 それを計算してみようという試み。

小５ 算数 小５ ５４ 正多角形 Youtube

八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋

 問2）右図のように、 abcがあり、点dは辺ab上の点である。 下の条件の①、②をともにみたす点pを、定規とコンパスを使って作図しなさい。 ただし、作図に使った線は残しておくこと。 条件 ①線分apの長さは、線分adの長さと等しい。第47問 正方形と正八角形 図形ドリル 6年生 正八角形 正方形 ★★★★☆☆（中学入試難関校レベル） 思わず「お～～！！」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは，色々なタイプの図形問題を取り上げています。 一辺の長さを100にしますので、キーボードから「100」と入力し「Enter」または「Space」で実行をします。 ⑥一辺100の正五角形が完成しました。 参考記事 ・作図補助機能（直交モード・ダイナミック入力）AutoCAD作図の基本 目次へ戻る 4．まとめ

角形 E An Design

正多角形 Wikiwand

カテゴリ一覧 他の勉強がしたい方はこちら 構造力学の基礎; 直線定規とコンパスを使う作図方法を2つ。 三角定規の角度や分度器や直線定規の数字を使う描き方は特に解説しません。 正八角形の条件 ・8辺の長さが等しい多角形。 ・8個の内角がそれぞれ等しく135度（八角形の内角の和は1080度）。 は一辺の長さの半分、 は対角線の長さの半分ですね。 正五角形 以前の記事「36°の三角比」で求めたように、 なので また となります。 正六角形 外接円の半径 と一辺の長さ は等しいですね。 正八角形 前回求めたように なので となります。

機械設計のための基礎製図

辺の長さが決まった正多角形をかく ５年生 算数の広場

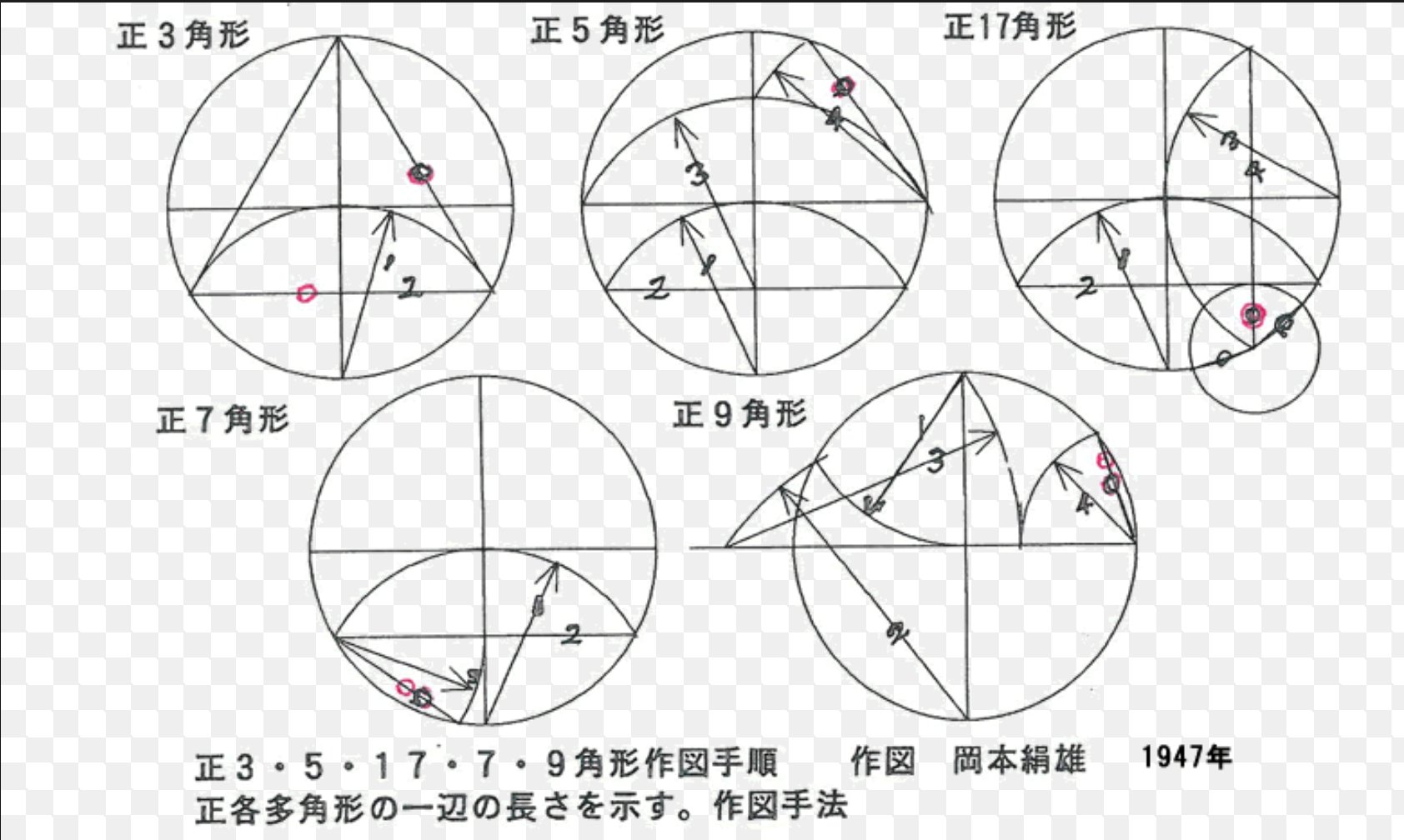
半径1の円に内接する正34角形の一辺の長さを作図して描きます o を中心とし、aa' を直径とする円をかく。 aa' に直交する半径bo をとり bo を 31 に内分する点を c とおく。 図のように d, e とおく。 ob 上に点 f を of = ad となるようにとる 円fo と afの延長との交点を g とおく。 ag の中点を h と手書きで、正八角形を描く方法を紹介します。 直線定規とコンパスを使う作図方法を2つ。 三角定規の角度や分度器や直線定規の数字を使う描き方は特に解説しません。 正八角形の条件 ・8辺の長さが等しい多角形。 ・8個の内角がそれぞれ等しく135度（八角形の内角の和は1080度）。 ・中(5) 辺ADは円周を7等分する基準長さとなるので，円周を7等分できる。 (6) 正7角形を作図する。 付図31 正7角形の作図 補足同様の作図法で，直径ABをn等分すれば，正n角形を作図できる。付図32は正9角形及び正5角形を作図した例である。ただし，n=3，4，6

460 ｘ460cmの正四角形の中に正八角形を書いた場合 1辺の長さは何 Yahoo 知恵袋

正七角形の作図 教材作家

正三角形 866（/100） 180° 60° 正四角形 7071（/100） 360° 90° 正五角形 5878（/100） 540° 108° 正六角形 50（/100） 7° 1° 正七角形 4339（/100） 900° ° 正八角形 37（/100） 1,080° 135° 正九角 正五角形の一辺の長さを作図するには、長さがわかっていた方がいいですね。長さを測る道具が使えないので半径 OA が何cmなのかはわかりませんが、作図には必要はないので問題ありません。作図に必要なのは、 OA の長さに対して、正五角形の一辺の長さがいくらか、です。比がわかれ 正多面体は、正四面体、正六面体、正八面体、正12面体、正面体の5種類しかない。 正四面体と立方体は簡単にできる。 これをもとに、他の立体を作図してみよう。 まずネットでそれぞれの多面体を調べてみよう。 どう作図できるか浮かんでくる。 さらに、全ての面が同じ形の多面体を

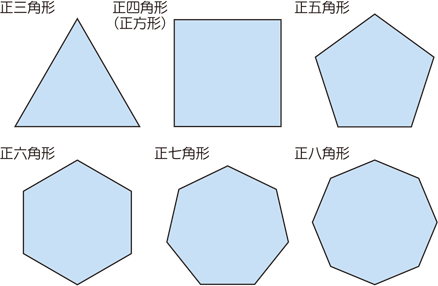
正多角形 算数用語集

１辺の長さが４ｃｍの正八角形の面積を求めよ という問題があるの 数学 教えて Goo

 どう作図できるか浮かんでくる。 さらに、全ての面が同じ形の多面体を作ってみよう。 正12面体と正面体については基本形を作ってみた。 参考 コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく 正八 角形 の 書き方

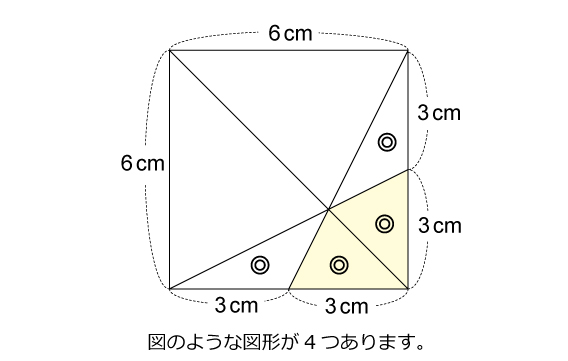
第47問 正方形と正八角形 図形ドリル 第47問 正方形と正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦

2

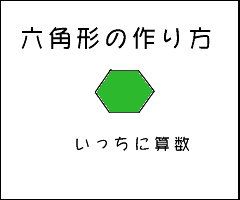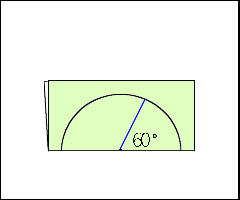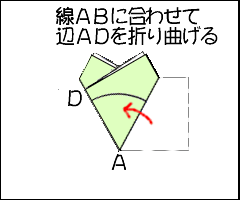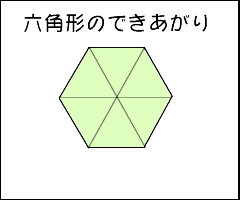
５年算数 正多角形と円周の長さの教え方

正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム

コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

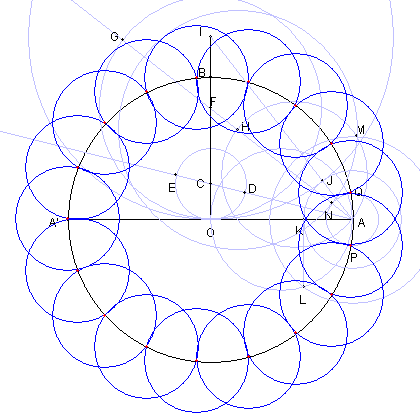
正１７角形の作図

コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫

正多角形作図不可能証明の齟齬 ２p N 正多角形の一辺の長さ 弦長 発想力教育研究所 素数誕生のメカニズム

コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

小学5年生 正多角形 算数 Active Learning 学院

第47問 正方形と正八角形 図形ドリル 第47問 正方形と正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦

正５角形の作図

５年算数 正多角形と円周の長さの教え方

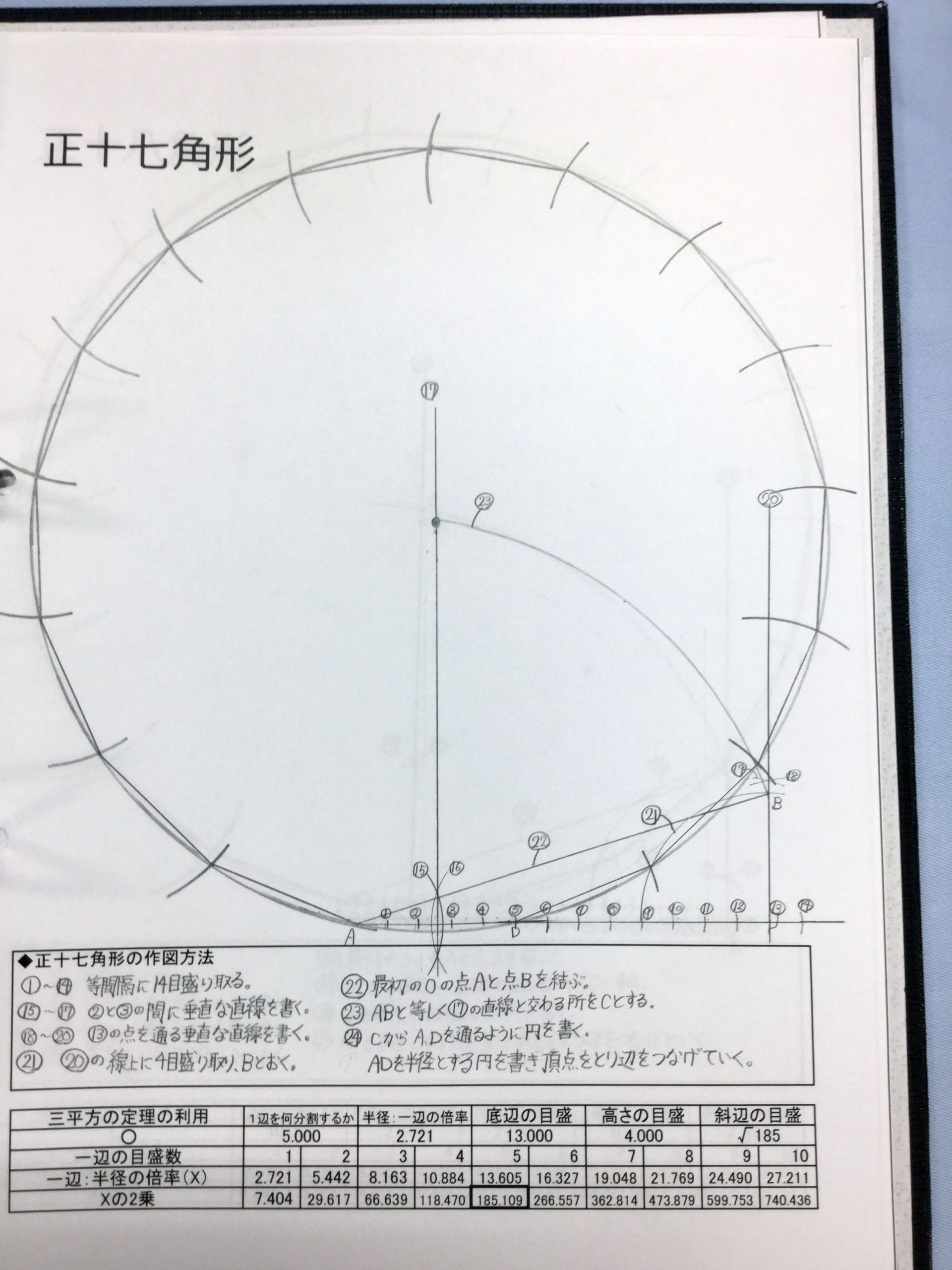
正多角形と私 慶應義塾普通部

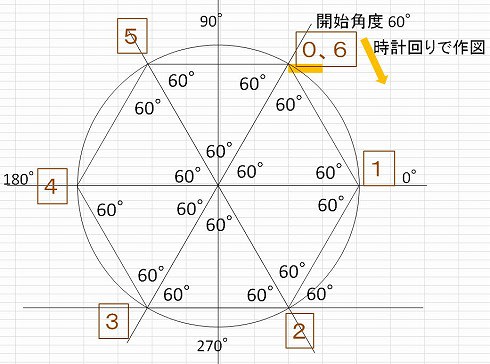
サッカーボールの型紙 エクセルvbaで正六角形を作図しますpart 2 日だまりのエクセルと蝉しぐれ

八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋

５年算数 正多角形と円周の長さ わかる教え方

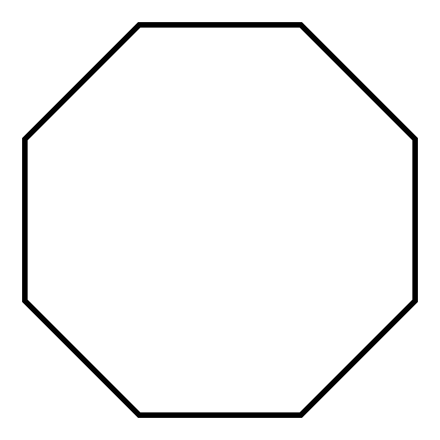
八角形 Wikiwand

七角形 Wikiwand

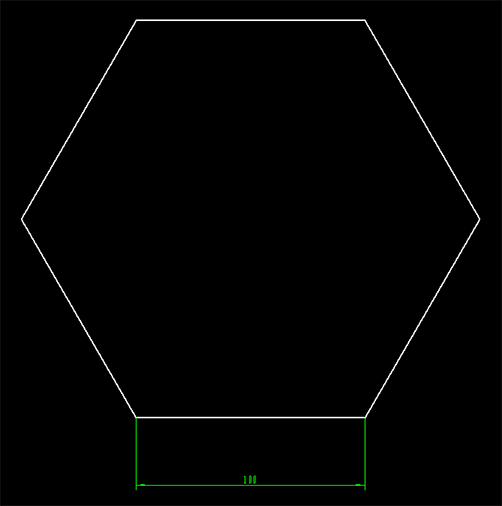
正多角形 Ironcad ユーザーガイド

正五角形の作図法 数理女子

発展 円に内接する正五角形の作図 デザインあ おとなスペシャルで紹介されてたやつ なかけんの数学ノート

正七角形の作図 教材作家

正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information

５年算数 正多角形と円周の長さの教え方

正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information

半径ａの円に内接する正八角形の面積の答えを計算式とともにお願 Yahoo 知恵袋

円に内接 外接する正多角形の周の長さを求める公式を作ってみよう 数学について考えてみる

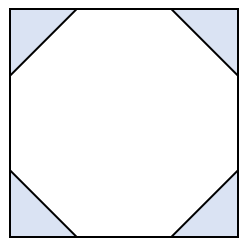
中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ

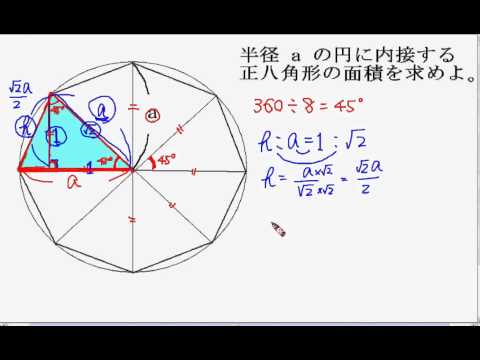
中３数学 正八角形の面積 Youtube

コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

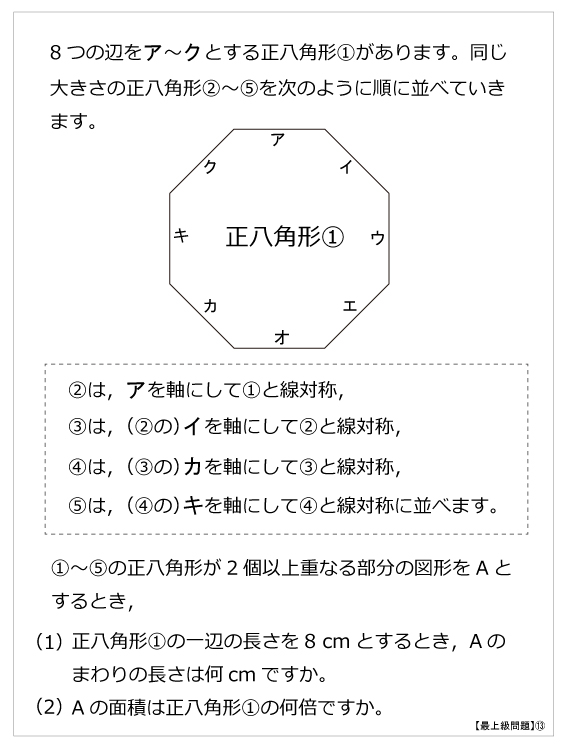
正八角形の問題 最上級問題 正八角形の問題 算数星人のweb問題集 中学受験算数の問題に挑戦

正多角形の描き方

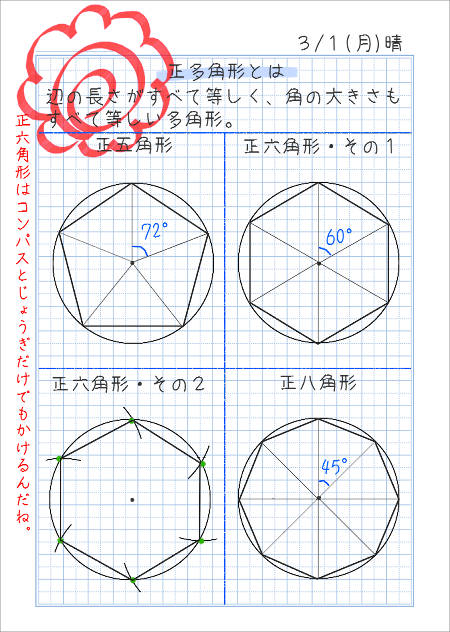
いろいろな正多角形をかいてみよう 家庭学習レシピ

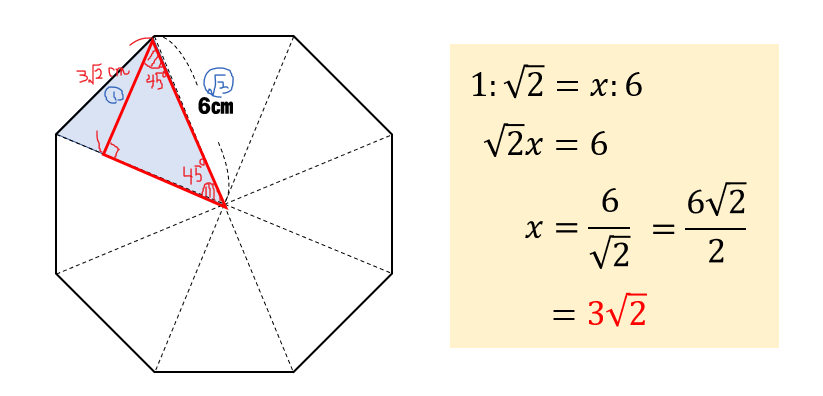
中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ

いろいろな正多角形をかいてみよう 家庭学習レシピ

正５角形の作図

中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ

コンパスと定規を使った七角形 正多角形 の描き方 図形の描き方016a 夏貸文庫

小学5年生 正多角形 算数 Active Learning 学院

コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫

正多角形２

機械設計のための基礎製図

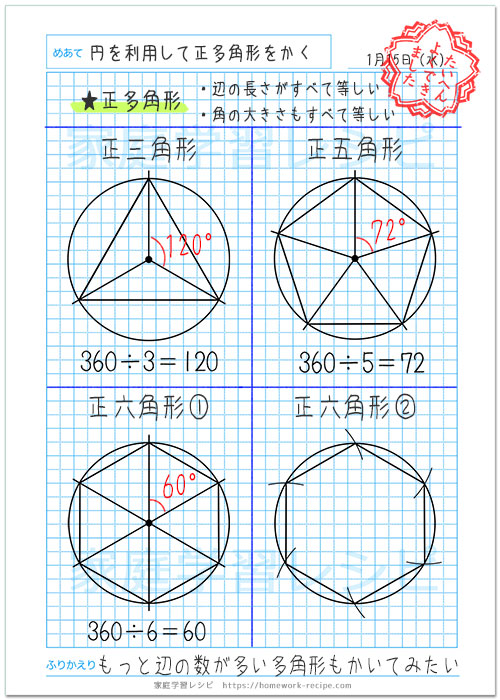
円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ

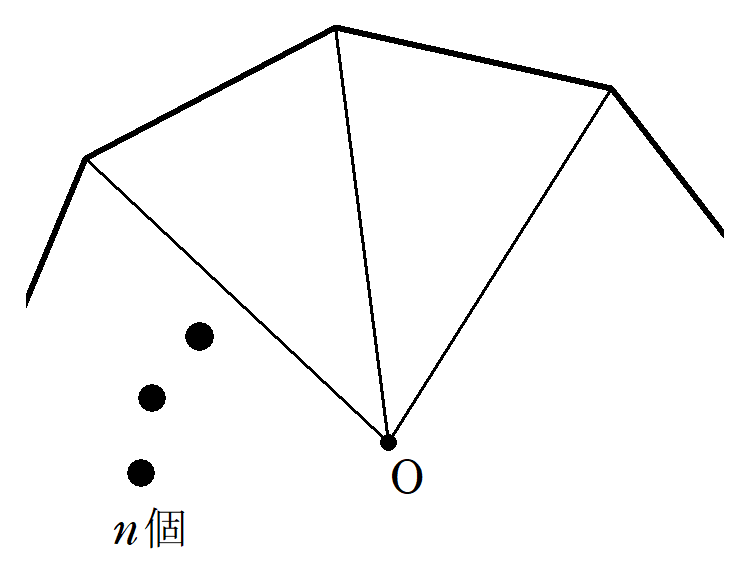
正多角形の面積の公式 一辺 A の正 N 角形の面積は１つの式で表せる Fukusukeの数学めも

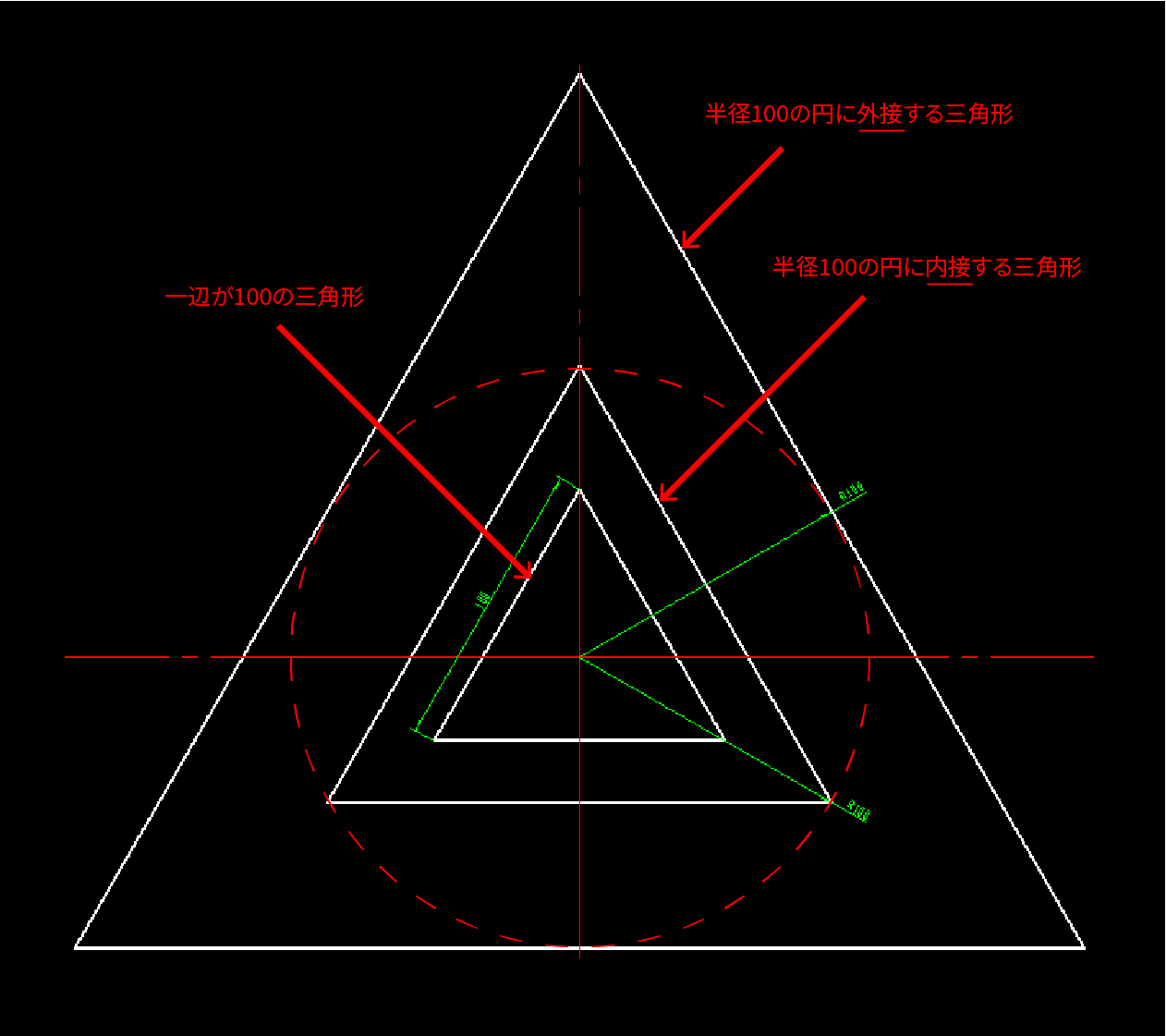
正多角形 Ironcad ユーザーガイド

正多角形 Ironcad ユーザーガイド

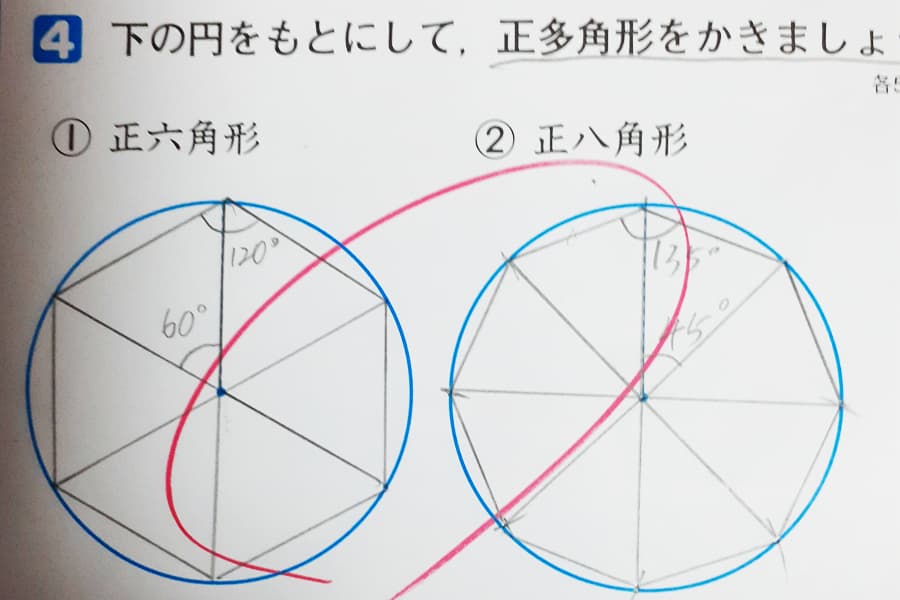
円周率は 3 00 以上であることを証明せよ 受験算数入門

一辺の長さが3cmの正八角形はどうやってかけますか 教えてください お願い Yahoo 知恵袋

５年算数 正多角形と円周の長さ わかる教え方

定規とコンパスを使って

作図 授業がんばりmath

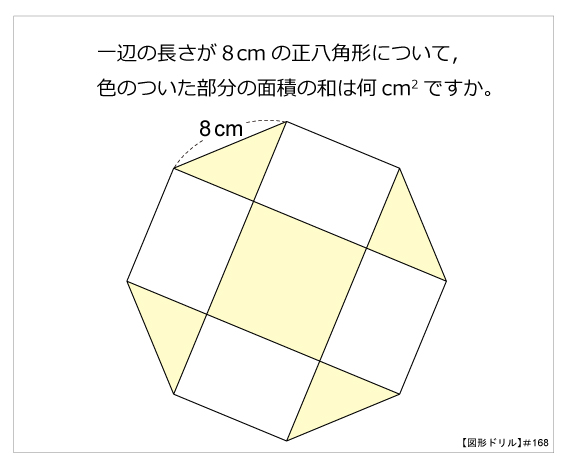
第168問 正八角形と面積の和 図形ドリル 第168問 正八角形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦

1

形態の基礎理論 三角形の重心

2

Kaizu Blog Excel半径で作図した正多角形の面積計算

正十七角形の作図

コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫

機械設計のための基礎製図

機械設計のための基礎製図

八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋

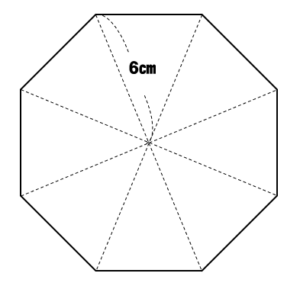
中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ

正多角形２

正多角形 Wikipedia

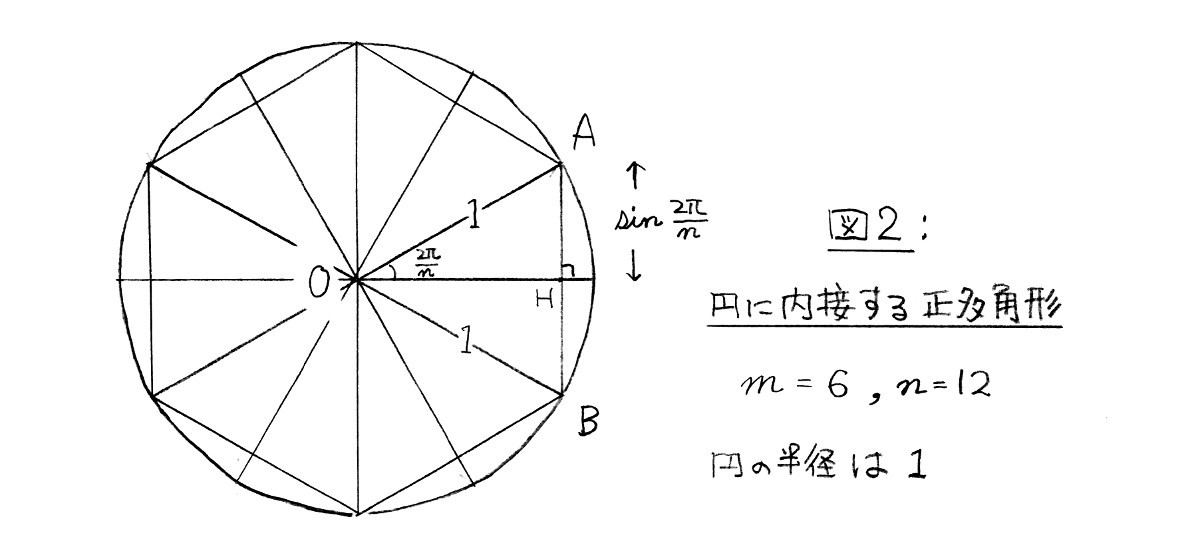
弧度と三角関数の極限２ 極限 Wandering In The Woods

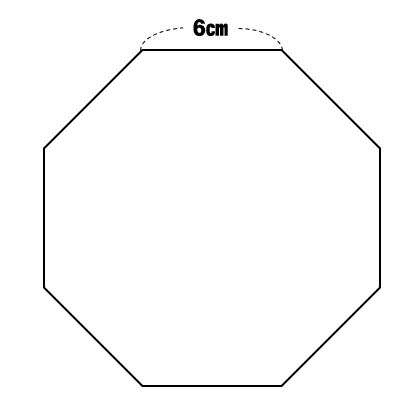
中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ

円に内接 外接する正八角形の周長と面積から円周率との関係を考える 数学について考えてみる

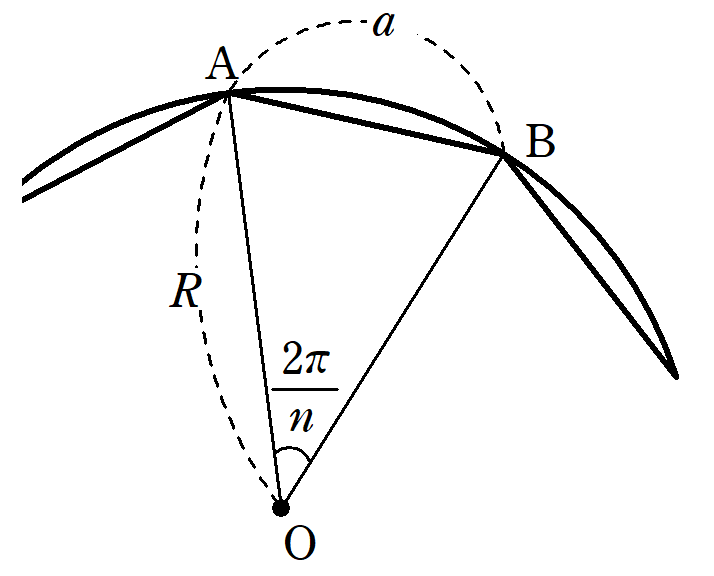
正多角形の面積の公式 一辺 A の正 N 角形の面積は１つの式で表せる Fukusukeの数学めも

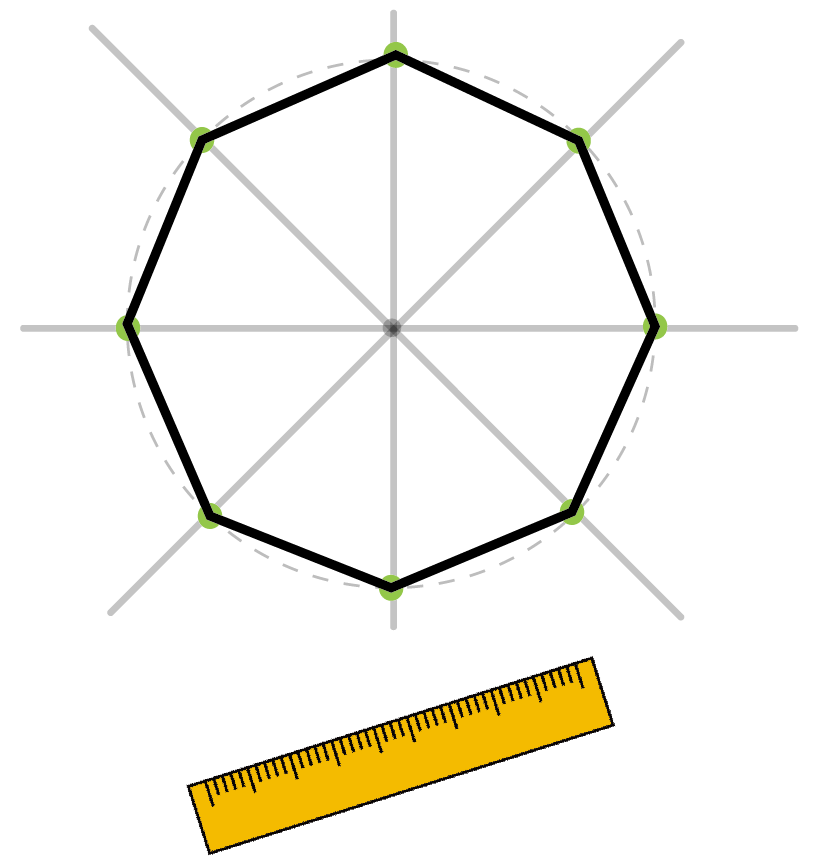
コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

小学5年生 正多角形 算数 Active Learning 学院

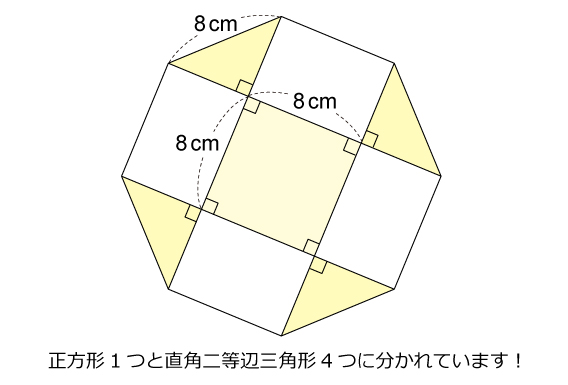
第168問 正八角形と面積の和 図形ドリル 第168問 正八角形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦

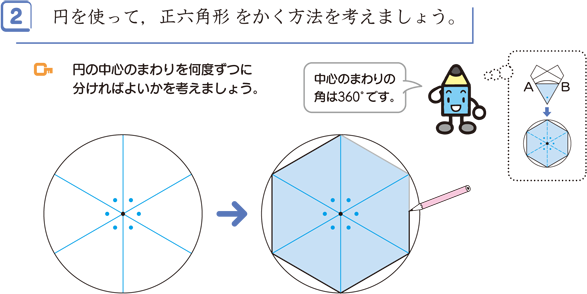
正多角形 算数用語集

円に内接する正八角形の書き方 合ってますか 円はあらかじめあります Yahoo 知恵袋

2

コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

定規とコンパスを使って

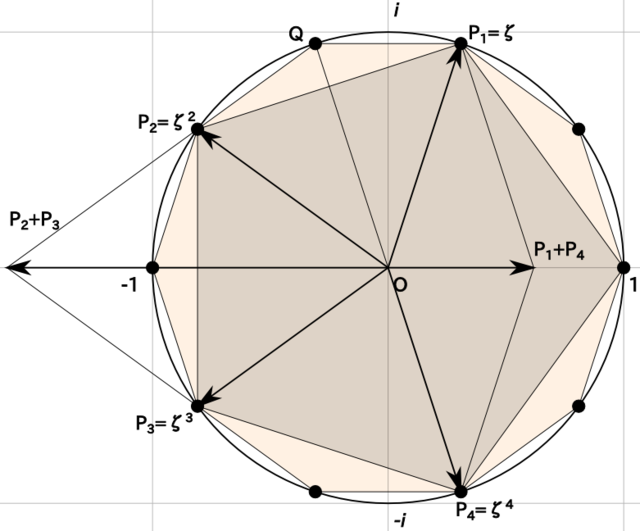
半径1の円に内接する正n角形の一辺の長さ 元祖ワシ的日記

正多角形作図不可能証明の齟齬 ２p N 正多角形の一辺の長さ 弦長 発想力教育研究所 素数誕生のメカニズム

５年算数 正多角形と円周の長さの教え方

正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information

Kaizu Blog Excel半径で作図した正多角形の面積計算

ケンジくん ハリガネの呪い 円に接する正多角形の書き方を使って 円を等分するシートを作りました 中心に空けた穴に円パーツの中心を合わせると均等に分ける線が引けます パイプにも使用可能 対角線を繋げれば任意の大きさの多角形も描けるので重宝

1

正八角形の作図 正方形から正八角形の作図の仕方を教えてください 数学 教えて Goo

1

正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information

コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫

コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

Incoming Term: 正八角形 一辺の長さ 作図,